¶ Probleme durch Selbstreferenz
- Dieser Satz ist falsch.
- „Du kannst einen Barbier definieren als ‚jemanden, der all jene, und zwar nur jene, rasiert, die sich nicht selbst rasieren‘. Die Frage ist: Rasiert der Barbier sich selbst?“ Quelle: https://de.wikipedia.org/wiki/Barbier-Paradoxon
¶ Halteproblem
Das Halteproblem ist ein grundlegendes Problem der Informatik: Es fragt, ob es einen Algorithmus gibt, der für jedes beliebige Programm und jede Eingabe entscheiden kann, ob das Programm irgendwann anhält oder unendlich weiterläuft.
Das Halteproblem ist ein grundlegendes Problem der Informatik: Es fragt, ob es einen Algorithmus gibt, der für jedes beliebige Programm und jede Eingabe entscheiden kann, ob das Programm irgendwann anhält oder unendlich weiterläuft.
Gegenbeweis durch Selbstreferenz.
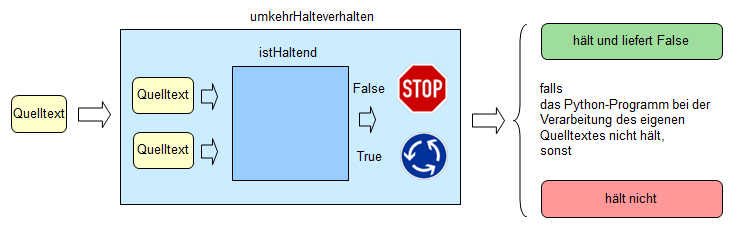
Your content here
Beweisidee zum Halteproblem (vereinfacht):
- Angenommen, es gibt ein Programm H, das für jedes Programm P und jede Eingabe E entscheidet, ob P(E) anhält.
- H(P, E) gibt also „hält“ oder „läuft endlos“ zurück.
- Wir konstruieren daraus ein neues Programm D:
- D(P) fragt H(P, P).
- Wenn H sagt „P hält“, dann läuft D absichtlich endlos.
- Wenn H sagt „P läuft endlos“, dann hält D sofort an.
- Nun betrachten wir D(D):
- Falls D(D) anhält → laut Definition läuft es endlos.
- Falls D(D) endlos läuft → laut Definition hält es an.
- Widerspruch in beiden Fällen.
- Also kann das Programm H nicht existieren.
- ⇒ Das Halteproblem ist unentscheidbar.